Developing a Gaussian Processes, using a Bayesian Network, Text Analysis algorithms and Fuzzy Logic Controller for a commercial Greenhouse
Abstract
Our lives in the planet is always under the constant threat of extension from natural and un-natural sources of agony. There is a need to adapt and survive better. At the core off the survival is the component of learning. This has now been achieved by the advent of machines that are able to make work easier for us humans. On the other hand is the availability of data all over the world that we use and access daily. The data is everywhere, and there are several sources for the data. The question remains to be what can be done with data to achieve what is needed for the survival in this modern times. Hence, the machine learning perspective would be a better consumer of the data, learning from the data and giving important insights from the data that help us live better.
A fresh data collection is like a well-wrapped present. It’s a collection full of promise and expectations for the wonders we’ll be able to do once you have figured it out. However, until you open it, it stays a mystery. One of the most frequent data mining jobs is predictive modelling. It is the act of collecting historical data, that is the past, finding data in the patterns using some techniques (the model) and then using the model to make predictions about what will happen in the scoring of new data as the name suggests.
The primary goal of this article is to describe some of the approaches that may be utilized to address these contemporary issues. For topic modelling, machine learning techniques include Gaussian Regression and classification, Bayesian Networks and Latent Dirichlet Allocation, are all utilized. The second section of this application looks at how fuzzy logic systems may be used to manage a greenhouse for optimum performance. He fuzzy logic designer tool box as used to create the fuzzy logic system in MATLAB Software. The Mamdani and Sugeno Inferences are the fuzzy logic inference methods utilized here. Because the linguistic intervals may be specified on the trapezoidal surface rather than the linear triangle surface in the Sugeno Model, the Mamdani inference method produces more crisp bounds.
PART I
Applications of the Gaussian Regression, Gaussian Classification, Bayesian Networks and Topic Modelling
Introduction
Our lives in the planet is always under the constant threat of extension from natural and un-natural sources of agony. There is a need to adapt and survive better. At the core off the survival is the component of learning. This has now been achieved by the advent of machines that are able to make work easier for us humans. On the other hand is the availability of data all over the world that we use and access daily. The data is everywhere, and there are several sources for the data. The question remains to be what can be done with data to achieve what is needed for the survival in this modern times. Hence, the machine learning perspective would be a better consumer of the data, learning from the data and giving important insights from the data that help us live better.
We need to look at models that can be used to analyze data and extract content from it, which will be helpful in addressing these modern-day issues. To acquire knowledge and ideas, the data must be examined by looking for unexpected patterns and anomalies. Exploration aids in the discovery process’ refinement. If visual exploration fails to show obvious patterns, statistical methods such as component analysis, correspondence analysis, and clustering may be used to investigate the data. Clustering, for example, may show groupings of consumers with different ordering habits in data mining for a direct mail campaign.[1].
To concentrate the model selection process, the data may be further changed by generating, selecting, and changing variables. You may need to modify your data to add information, such as customer grouping and important subgroups, or include new variables, based on your findings in the research phase. It’s possible that you’ll need to search for outliers and decrease the number of variables to get down to the most important ones. When the “mined” data changes, either due to fresh data being accessible or newly found data problems, you may need to alter the data. You may change data mining techniques or models as new information becomes available because data mining is a dynamic, iterative process.
Modern machine learning techniques also enable us to model data by enabling software to automatically search for a set of data that consistently predicts a desired result. Neural networks, tree-based models, logistic models, and other statistical models, such as time series analysis, memory-based reasoning, and principal components, are examples of data mining modeling methods. Each model has its own set of capabilities and is best used in certain data mining scenarios based on the data. Neural networks, for example, excel at fitting extremely complicated nonlinear connections. Finally, we must evaluate the data by determining the relevance and trustworthiness of the data mining results, as well as estimating how well it works. You may also test the model against known data. If you know which consumers in a file have a high retention rate and your model predicts retention, you may test if the algorithm correctly picks these customers. In addition, practical applications of the model, such as partial mailings in a direct mail campaign, help prove its validity [2].
1. Problem statement
Within the limits and extent of the life of a human being, we encounter events and should be able to learn from them. The human brain I however multidimensional and present that it finds it hard to be able to extract patterns using the bare eyes or by intuition. It is with this great drawback that we have to resort to using other means for solving the problems we encounter in day to day activities. The aim of this paper is to be able to solve these problems using machines. Machines are able to use algorithms to learn from the data and give us what we expect or an understanding into an event that is already ongoing.
2. Objectives
- To develop a work flow that enhances the Gaussian processes, that is the Gaussian regression and the Gaussian classification.
- The Bayesian network are to be investigated for their use in the area of classification.
- The use of the Latent Dirichelt modelling for carrying out text analysis.
3. Datasets Used
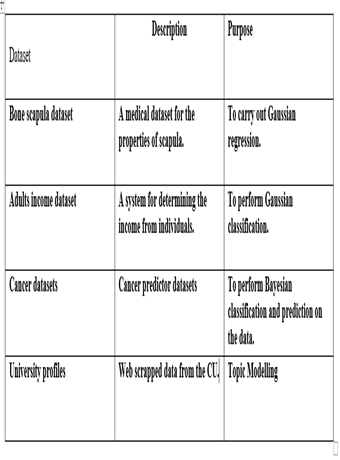
Figure 1 Datasets used for the analysis
An overview of the datasets is shown below with the Pandas library.
The bone scapula dataset.
Figure 2 Scapula dataset
The scapula dataset was obtained from https://www.kaggle.com/iham97/deepscapulassm
Adults Income
The adult’s income dataset was obtained from https://data.census.gov/cedsci/all?q=adult%20income
Figure 3 income datasets
Cancer datasets
The data was obtained from https://www.kaggle.com/uciml/breast-cancer-wisconsin-data
Figure 4 Cancer datasets
Finally is the Coventry University profiles data that had to be web scrapped first.
https://pureportal.coventry.ac.uk/en/organisations/faculty-of-engineering-environment-computing/persons/?page=1
Figure 5 Coventry University dataset
4. METHODOLOGY
All the procedures that have been carried out in order to have the desired results for the applications have all been pre-processed and finally used in different mechanisms. There is also text data that has been used for topic modelling.
4.1 Gaussian Regression
The Gaussian probability distribution is generalized to form a Gaussian process. A stochastic process controls the characteristics of functions, while a probability distribution governs the attributes of scalars or vectors (for multivariate distributions). Without getting too technical, a function may be thought of as a very long vector, with each element indicating the function value f(x) for a certain input x. Although this concept is a bit naive, it turns out to be remarkably close to what we need [3].
Gaussian process (GP) regression models may be interpreted in a number of ways. A Gaussian process may be thought of as defining a distribution over functions, with inference occurring directly in the function space [4]. A Gaussian process is defined as a collection of random variables is defined as a Gaussian process. As a result, the definition implies an inherent consistency condition, often known as the marginalization property. The processes utilized to process the data, from pre-processing through constructing the model, are shown and described below. The Gaussian Regression application starts with the importation of the libraries and getting the file needed from the root folder.
Figure 6 Get the libraries and get the csv file
The datasets here looks clean and there is no need for any further data cleaning process that should be done to it further. We can check the columns of the data.
Figure 7 The data frame of the scapula data
For any machine learning algorithm there needs to be a test dataset and a training dataset. In the case where the data collection samples or population were not created separately as training and testing, then we have to create the datasets. To do this is however, not hard. We need to split the data into training and testing respectively. This is done using the train split test, where the data can be split into 30% for testing and the other 70% for testing.
Figure 8 Define the targets and the predictors
The next step is to use the Gaussian regression to fit a model that can be used for the predictor variables. It is important to note that a kernel is a very important part of the regression and therefore has to be defined.
Figure 9 Fit and predict the Gaussian regression
The most crucial part that follows is to determine how much the regression is successful in predicting the values of the independent variable. In order to come to this conclusion, we have to use the accuracy test score.
Figure 10 Gaussian regression accuracy score
The score for the regression procedure is a bit lesser than expected, although still showing a correlation between variables in the scatter plot. Other methods of regression should be exploited in order to understand how well the Gaussian regression model performs.
4.2 Gaussian Classification
It’s more difficult to utilize Gaussian processes to solve classification difficulties than it is to address regression problems. This is because the likelihood function was Gaussian; when a Gaussian process prior and a Gaussian likelihood are combined, a posterior Gaussian process over functions is generated, and everything remains analytically tractable [3]. When the objectives are discrete class labels, the Gaussian likelihood is inappropriate for classification models [5]. In the regression case computation of predictions was straightforward as the relevant integrals were Gaussian and could be computed analytically. In classification the non-Gaussian likelihood makes the integral analytically intractable [6]. Bayesian classification depends on the higher values value of the back propagated chance values [5].
In the next steps below, the Gaussian classification is to be applied on the ADULTS dataset. The dataset is an interesting application to indicate how the Gaussian methods can be applied in the classification of the binary data. We also intend to predict whether an individual will be able to make a salary of $50,000 on an annual basis.
Figure 11 To begin with is getting the libraries needed
The data has a lot of data cleaning to deal with. This is important because at the end we want the data to be in the same dimensions or shape. The data contains 9 categorical variables and 6 numerical variables.
Figure 12 Categorical variables
Replacing the values of rows that are null or removing them is considered in making the data useful.
Figure 13 Replace null values
The data is finally clean and can be used for the data analysis. Before proceeding, it’s important to check on the numerical variables and how many labels exist in the categorical variables.
Figure 14 Numerical columns and final clean data frame
The next step is to split the data frame into the dependent and the independent variables. The dependent variable here being the income data. The other values in the data frame are used to determine the values of the income data.
Figure 15 Split dataset into training, testing,
The train test split has also been applied on this dataset in order to create a testing and training dataset from it. The training data is larger, being 70% and the testing data is 30%.
The next step is to carry out the classification using the Gaussian Naïve Bayes. The model then predicts the values that were split, and names the x test dataset.
Figure 16 Predict the incomes
In order to know how well the model performed, we need some metrics to evaluate the performance. The accuracy score is evaluated on how well the model performs on the test and the training datasets.
Figure 17 Accuracy scores for the classifier for income
The results show that the prediction carried out on the test data and the training data are relatively the same. Our model indeed makes sense. There is only a slight difference between the two meaning, that the larger training data can predict a test values at 80.21%.
4.3 Bayesian Networks
Both supervised and unsupervised learning may be accomplished using Bayesian networks. Because there is no goal variable in unsupervised learning, the only network structure available is DAG [4]. In supervised learning, we just require the variables that are close to the goal, such as the parents, children, and other children’s parents (spouses). Other network topologies include tree augmented naive Bayes (TAN), Bayesian network augmented naive Bayes (BAN), parent child Bayesian network (PC), and Markov blanket Bayesian network (MBBN) (MB). The types of connections that may be made between nodes vary across these network topologies. The three kinds of connections (from target to input, from input to target, and between the input nodes) and whether or not to allow spouses of the target are used to categorize them.
The Gaussian naive Bayes classifier is the most frequent kind of naive Bayes classifier. We assume that the probability of feature values, x, given an observation is of class, y, in Gaussian naive Bayes [7].
The Breast Cancer dataset has been used to illustrate how well the Bayesian Network perform. The code begins with the importation of the libraries needed for the Bayes networks.
Figure 18 Bayes libraries
It is also important to note that the joy and usefulness of applying the machine learning algorithms, especially for supervised learning, is that they can be compared and the best that performs be determined. The same is applied for this case where the algorithms are compared to determine which performs better against the Bayesian algorithms.
The data can now be imported and describes. The data has 30 columns, all of which, except the unknown column care used as indicators for the prediction of breast cancer.
Figure 19 Import and describe the data
The heat map plotted below using sea born library is meant to indicate the relationship between the 30 variables.
Figure 20 Correlation matrix with heat maps
Just like before where we had no training or testing data to use, the cancer data has to be split into testing and training using the train split test method.
Figure 21 Split into testing and training for Bayes
The next step is to define the models that will be used to predict the probability of a patient suffering from breast cancer. The algorithms are all run and their accuracies later compared.
Figure 22 Models scores for prediction
The Bayes algorithm performs the best here. As mentioned before, that for data with several columns and rows, the Bayes perform better, and indeed this is proof.
Figure 23 Performance comparison
4.4 Text Analysis
Language-aware features are data products developed at the confluence of research, experimentation, and practical software development. Users immediately encounter the application of text and voice analysis, and their responses give input that helps to customize both the application and the analysis. This virtuous loop is typically naïve at first, but it may develop into a complex system with rewarding outcomes with time[8]. The practice of allocating text documents to one or more classes or categories, given that we have a predetermined set of classifications, is known as text or document categorization. Documents are linguistic documents that may include a single phrase or even a paragraph of text.
Tokenization is the initial stage in the process. Sentence tokenization is the process of dividing a text corpus into sentences, which serve as the corpus’s initial level of tokens.. Any text corpus is a collection of paragraphs, each of which contains multiple phrases [8].
This is followed by a process called normalizing.. Cleaning text, case conversion, fixing typos, eliminating stop words and other superfluous phrases, stemming, and lemmatization are some of the additional methods [9]. Text cleaning and wrangling are other terms for text normalization. The next stage is to obtain the stem of the words, which is known as stemming. For instance, while eating, the stem gets consumed.
After stemming, the lemmatization procedure may begin. Lemmatization is similar to stemming in that you eliminate word affixes to get to the word’s basic form. The root word, also known as the lemma, is always found in dictionaries.
Topic modeling entails extracting characteristics from document terms and utilizing mathematical structures and frameworks such as matrix factorization and SVD to create identifiable clusters or groupings of terms, which are then grouped into topics or ideas. These ideas may be used to decipher a corpus’ primary themes and to establish semantic links between terms that appear often in different texts [9].
The solution for the topic modelling in this paper is done using the CU profiles. These contain the author names and the publications they have made. The major topics form the publications are obtained using the Latent Dirichlet Allocation method.
Figure 24 Import the libraries and the data
I also had to filter the data so the columns remaining are the ones intended for use in the topic modelling part.
Figure 25 Filter the columns
The next step is to download the stop words from NLTK and create a vectorised version of the dataset.
Figure 26 Download the stop words and extract the features
Finally, the vectors create by the IT-IDF can be used for generating topics using the Latent Dirichlet Allocation method.
Figure 27 Topic Modelling
PART II
FUZZY LOGIC CONTROLLER FOR A GREEN HOUSE
1. FUZZY LOGIC
The meaning of fuzzy logic can be divided into two broad categories or terms. There are basically two types of systems that can be explored in a global sense, these are the classical sets and the fuzzy sets. Fuzzy logic relates to the fuzzy sets, this theory is based on classes of objects with non-sharp boundaries also known as membership values. A fuzzy set contains the elements that have a varying degree of membership in the set. This means that larger values mean a higher degree of membership and lower values denote a lower degree of membership. Such sets are known as the membership functions and the set is defined by the fuzzy sets. A fuzzy set can then be defined as the set containing the elements having varying degrees of member ship in the set.
Figure 28 Membership functions of a set
The idea of using membership functions is different with the crisp idea because with the crisp set, the member are either complete members or not members at all. The members of a fuzzy set do not have to be complete but can still belong to a certain category. Fuzzy sets are assigned numbers in the range from 1 to 0.
1.1 Membership functions
The property of fuzziness in a fuzzy set is characterized by the membership functions. There are different methods that are used to form the membership functions. The support defines the non-zero members that live inside the set. The boundary defines the region that has non zero members but the members do not have full membership [10].
1.2 Fuzzification Process
This is a very important concept in the sphere of fuzzy logic as it involves the crisp values are converted into the fuzzy sets. The uncertainties in the crisp values are identified hence forming the fuzzy sets. In the broadest terms possible, there are always errors encountered for example in measuring temperature in a reactor industry. The errors in the data can also be modelled and represented by the membership functions, this is done by assigning the membership values to a certain given crisp quantities. There are several methods that can be used in the fuzzification process including intuition, inference, rank ordering, angular fuzzy sets, neural network systems and the use of inductive seasoning [11].
1.2.1 Intuition
This is based on the application of a human beings own intelligence in order to develop the membership functions.
1.2.2 Inferences
The use of deductive reasoning is applied in this case. The membership functions are formed from the use of facts and known knowledge [10].
1.2.3 Rank Ordering
The use of poles is applied to assign the membership functions to the values by using a rank. Preferences are set down for double comparison and then from there the ordering for the membership is done.
1.2.4 Use of angular fuzzy sets
The angular fuzzy sets are applied in quantitative description of the linguistic variables for a set of already known truth values. For example when it has been established that the membership value of 0 is false and the membership value of 1 is true, then the values in between 0 and 1 are known as partially true or partially false [10].
1.3 Defuzzification
This refers the conversion from the fuzzy sets back to the crisp values. This process is necessary because the fuzzy results cannot be used as they are hence the quantities have to be converted back to the crisp quantities. The defuzzification has the ability to reduce a certain fuzzy set value back into the crisp values. The process of defuzzification is a necessary process because the output given by the systems cannot be delivered using the linguistic values such as very low, moderately high, very negative or any other description. The results have to be given as crisp quantities.
1.4 Formation of Rules in Fuzzy Systems
The use of rules form the basic working principle of the fuzzy logic systems. The rules form the linguistic results that are given by the inputs to the system. The fuzzy rule based systems sues he fuzzy logic systems. The rules form the linguistic results that are given by the inputs to the system. The fuzzy rule based systems uses the assignment statements, conditional statements and unconditional statements [12].
1.5 Fuzzy Inference Systems
They are also known as fuzzy rule-based systems, fuzzy expert systems or the fuzzy models. The systems are used to formulate a set of rules and from the set of rules, a decision can be made. The use of a fuzzy model in a controller necessitates the use of crisp values for the output. The fuzzy system consists of a fuzzification inference module which transforms the crisp values to the matching linguistic values, a decision making block that performs the heavy lifting of making an applying the rules, a state database and a defuzzification inference which is used to transform the linguistic values to the output crisp values.
Figure 29 A fuzzy inference system
The crisp inputs are converted into a fuzzy through the fuzzification method. The rule base is then formed, and together with the database they form the knowledge base [13].
1.6 Fuzzy Inference Methods
The two most common methods that have been used for the implementation of the fuzzy logic systems are the Mamdani’s fuzzy inference method and the Takagi-Sugeno-Kang method.
1.6.1 The Mamdani Inference Method
It is the most popular technique for implementing fuzzy set theory, and it requires fuzzy sets as output membership functions. It is feasible to utilize a single spike as the output variable that requires defuzification once the aggregation procedure has been completed on the fuzzified data. In many instances, a single spike may be utilized instead of a dispersed set, which is both feasible and considerably more efficient. For membership functions, this is known as the singleton output approach, and it may be a pre-defuzzified fuzzy set. A two-dimensional function’s centroid is found using the Mamdani technique [14].
1.6.2 The Takagi-Sugeno Method
Takagi, Sugeno, and Kang developed the Sugeno fuzzy model to formalize a system method for creating fuzzy rules from an input–output data set. Sugeno–Takagi model is another name for the Sugeno fuzzy model. For both approaches, the first two steps of the fuzzy inference process, fuzzification of the inputs and application of the fuzzy operator, are the same. The distinction is that the membership output functions in the Sugeno Inference system are either linear or constant. The Sugeno technique is excellent for serving as an interpolating supervisor of several linear controllers that are to be applied, respectively, to various operating conditions of a dynamic nonlinear system since each rule is linearly dependent on the system’s input variables. The performance of an airplane, for example, may vary significantly depending on altitude and Mach number. A Sugeno FIS is a natural and efficient gain scheduler that is ideally suited to the job of smoothly interpolating the linear gains that would be applied over the input space [11].
1.7 Fuzzy Logic System Implementation for Green House
The fuzzy logic system was developed using the Matlab Fuzzy Logic ToolBox. The application being implemented is for a Green House Controller. The Fuzzy system is developed by using the Mamdani and the Sugeno Inference systems. The greenhouse model has been optimized by using the Simulink package in Mat lab. The Simulation results obtained cab be related to the surfaces of the rules, which show the effects of varying the variables on the outputs. A greenhouse can have several instruments that can be used to realize these conditions. These devices are known as actuators. For the case of the three output values, there are thermometers for temperature and barometers for humidity for example.
1.7.1 Fuzzification of Inputs and Membership Functions
The view of the application is that it has been developed using the Mamdani model. The system has 6 input variables and 3 output variables. The output variables can be read using the actuators installed in the green house.
Figure 30 The greenhouse Mamdani model
The fuzzification is done after defining the membership functions of the system. The fuzzy set is a tool that allows representation of the members in a vague manner. The method is applied to convert the crisp values into the fuzzy sets. All the 6 input variables have been fuzzified. The fuzzification gives the input variables linguistic ranges that are then used to create the rules for the system.
Figure 31 Internal temperature variable
The values of the variable temperature have been used in the range of -10 to 10 degrees centigrade. The values are then converted to the linguistic versions as shown in the diagram above
The next variable is the external temperature of the green house system that can also be measured from the actuators, such as the thermometer.
Figure 32 External Temperature
The values of the external temperature range from 0 to 20 degrees centigrade. Then the values are further converted to the fuzzy sets of very low, low, zero, high and very high.
The next variable being used for the green house is the internal humidity. The values range from0 to 100. The actuators for the humidity can be incorporated inside the green house too.
Figure 33 Internal humidity
The variable light is used to check on the level of light within the green house that can sustain the process of photosynthesis.
Figure 34 Light variable
The light variable is further fuzzified into evening, morning and nigh times.
Seasonal cloud also determines the situations within the green house. The values range from 0 to 100. The values are important factor that affects the humidity within the green house.
Figure 35 Seasonal Clouds
The last input variable that has been used for the green house system is the outside humidity. The values can be measured using a barometer.
Figure 36 External humidity of the green house
The next variables that have to defuzzified for this case, are the output variables. The output variables have to be indicated as crisp sets rather than fuzzy sets. These variables include the temperature, humidity and the shade. This defines whether the inputs have given the optimum or the minimum shade.
Figure 37 The shade output variable
Another output variable is the temperature variable. This is quite straight forward and can be directly measured from the thermometer actuators.
Figure 38 Temperature output variable
The value of the humidity can be obtained from the cloud, temperature and lightness in the green house.
Figure 39 Humidity output variable
1.3 OPTIMIZATION OF THE FUZZY LOGIC CONTROLLER
The fuzzy system controller can be simulated using the Simulink tool box in Matlab. The system can be broken down further and the model run.
Figure 40 Model under mask
The mask option of the model allows us to inspect the input and output parameters of the FIS model.
Figure 41 Input variables and the rules
The Simulink Model looks a bit complex further with the output variables included later.
Figure 42 The output variables in the model
The models created have to be combined in order to have the optimized conditions for operating the greenhouse. The final combinations and defuzzification gives us up to 50 rules that can be applied or this case.
The membership functions need to be converted from their crisp sets and optimized as follows:
The values of Internal temperature had 5 optimization functions
The members of the External had five optimized rules functions
The values of the internal humidity had 5 optimization rules.
The values of the Light variable has 3 optimization functions.
The variable Seasonal cloud has three functions
The values of External humidity have been combined to have 5 output functions
These inputs will help us determine the number of rules to input for the system such that there is no repetition of the inputs. Each rule will represent a fuzzy logic rule.
Figure 43 Optimization of temperature inputs
They have all been combined and fuzzified so that we have fifty rules for the cimbinations.
Figure 44 Combining the clouds and light intensity
The surfaces have been used to illustrate how the optimization works. The Simulink library should be explored further to get the exact values.
Figure 45 Optimized perfomance for the rulesFigure 46 All rules combined have to be fuzzy
2.1 OPTIMIZATION SURFACES
The surface viewer is a very important tool in exploring the effects of varying a variable on the output variables.
2.2 SUGENO TYPE INFERENCES
The Sugeno model has been explored to be able to perform better in the case where we have a set of linear functions. It is able to deal well with the issue of non-linear functions.



